provide a detailed, preferably stepwise, account of
the performance of the method.
Analysis and optimization of analytical variables
The principal objective in the development of a
laboratory method is to end up with the maximum
possible analytical quality given the level of practica-
bility envisioned by the developers. To achieve this
goal, it is necessary to identify the optimal combina-
tion of operating set-points for the analytical
variables of the method. This requires an analysis of
the dependency of the quality endpoints upon the
operating set-points. Luque de Castro
et al.
performed an exceptionally thorough analysis of this
sort in the development of their method. They used
the magnitude of the analytical signal as the primary
quality endpoint and studied a variety of analytical
variables,
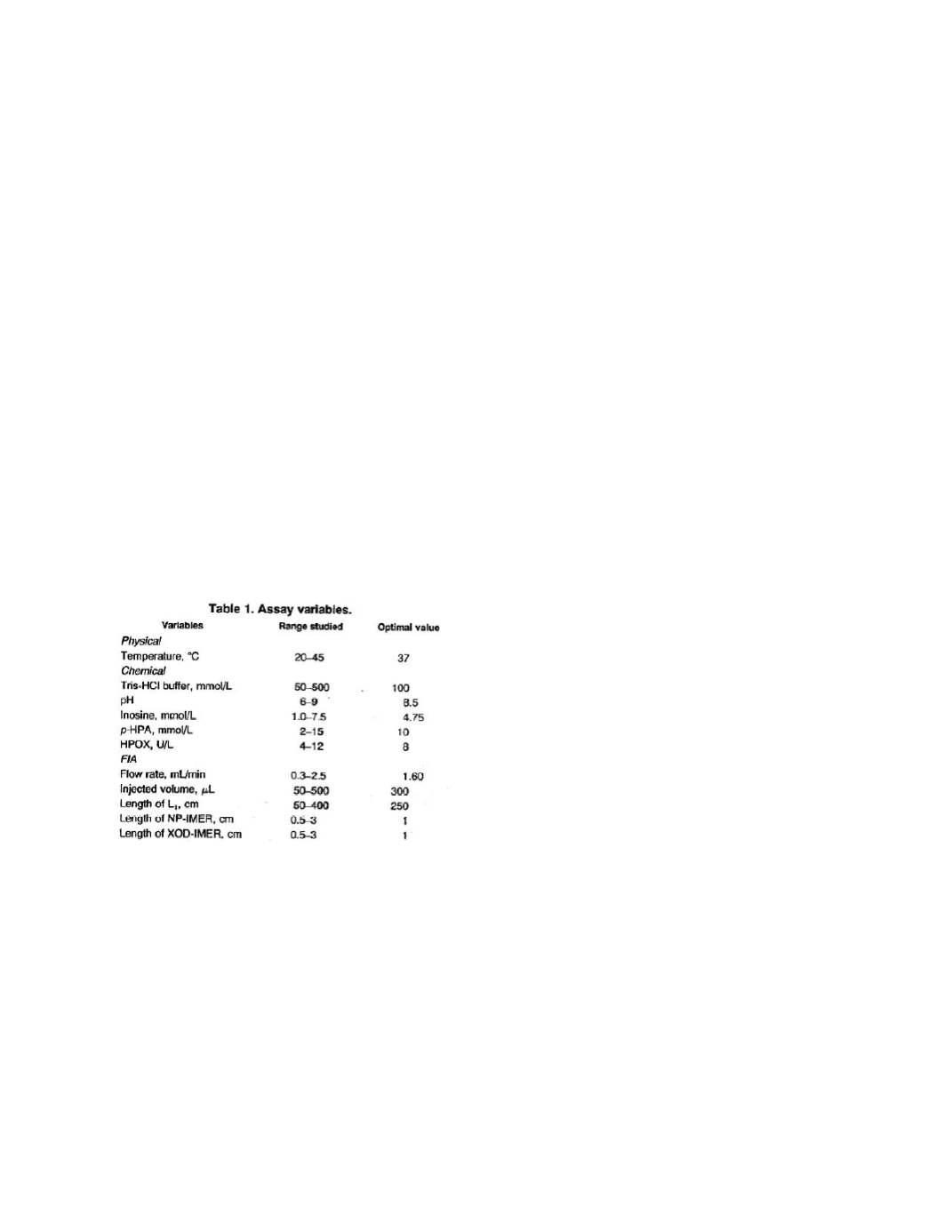
The variables affecting the analytical process
and hence the signal it provided were classi-
fied as chemical, physical, and hydrodynamic
(Table 1), and then studied by univariate
analysis.
The analysis and optimization of the flow injection
variables is described as follows,
High flow rates (2.32 mL/min) decreased the
analytical signal, but low flow rates (0.58
mL/min) decreased the sampling frequency
and resulted in increased dispersion. A flow
rate of 1.60 mL/min was selected as a
compromise.
A sample volume of 300 µL was chosen to
obtain the best analytical signal, since at
greater volumes the signal remained almost
constant.
The optimal lengths of the enzyme reactors
were 1 cm each. Using a longer NP IMER
provided a sharp increase in the baseline and a
decreased analytical signal. Increasing the
XOD IMER did not improve the analytical
signal.
A length of 250 cm for the open reactor was
enough to achieve a reproducible mixture of
reagent C and the main stream, thus providing
optimal analytical signal.
Notice that, even though the primary quality
endpoint was the magnitude of the analytical signal,
the flow rate that was selected as optimal was not the
flow rate resulting in the maximum value of the
signal. Larger signals were obtained at lower flow
rates. However, the lower flow rates decreased
measurement precision, a secondary quality
endpoint, and decreased the sampling frequency of
the system, a practicability endpoint. It is not infre-
quent in method development that the choice of an
optimal analytical variable set-point represents such
a compromise among competing quality and practi-
cability considerations.
A univariate approach to method optimization
was employed by Luque de Castro
et al.
In the
univariate approach, the response of a system to the
set-point of one variable is studied with all of the
other variable set-points held constant. This works
fairly well if all of the variable set-points are held
near to their true optimal values or if the sensitivity
of the system to the set-point of each variable is
largely independent of the set-points of the other
variables. It works poorly if the approximate values
of the optimal set-points are not known beforehand
and if there is interdependence among the variables
in their effect upon the system response.
A multivariate optimization approach can be
used in circumstances in which the univariate
approach is not likely to perform well. In the multi-
variate approach, none of the set-points of the
analytical variables are kept constant; instead, the
response of a system to various set-point combina-
tions is studied (Box and Draper 1987). The combi-
nations are chosen so that they will cover what is
a
priori
believed to be the most interesting portion of
the multivariate solution space. This provides data
points on the response surface, the multi-dimensional
surface that characterizes the relationship between
system response and the set-points of the analytical
Laboratory Methods
2-16


