other hand, one could argue that this probability of
detection is too small to justify the expense and
bother of screening.
Fortunately, screening studies can usually be
performed more than once. Indeed, periodic screen-
ing is the norm. In this way the probability of
detecting the disease in the subclinical phase can be
greatly increased (Eddy 1982). For instance,
continuing the preceding example, the effect of a
single screening study upon the natural history of the
hypothetical disorder can be computed and the
optimal timing of another study predicted. In this
example, the prevalence of subclinical disease
reaches a maximum 5 years following the initial
screening study, after which it decreases steadily.
Performing a second study in asymptomatic
individuals 5 years after the first, and using the same
critical value, will result in an identical impact on
the disease; 69 percent of the subclinical cases will
be identified and another 20 percent of cases shall
have been detected while in the subclinical phase.
Therefore, in this example, a second study can
double the yield of the screening program. Of
course, at the same time, the overall specificity of
the screening program will decrease slightly.
Additional increases in the number of screening
studies would further increase the probability of
detecting subclinical disease but at the price of
reducing the specificity even more. In order to
maintain an acceptable level of overall specificity for
a screening program, it is necessary either to set an
upper limit on the number of studies performed or to
adjust the threshold probability of diagnosis to take
into account the multiplicity of studies.
MONITORING PHYSIOLOGIC STATUS
The response of a clearance function marker to a
sudden, persistent change in organ clearance
function is illustrated in Figure 5-3. The time
course of the change in functional status is shown in
the upper graph. The function marker responds to
the drop in its clearance rate by accumulating in the
plasma until it reaches a new steady-state concentra-
tion as depicted in the lower graph. The rapidity
with which the new steady state is reached depends
upon the half-life of the marker; it takes 4-5 half-
lives for the steady state to evolve. For example,
the half-life of creatinine in the plasma in the setting
of normal renal function is 4 h. At 80 percent of
normal renal function, the half-life is 5 h. If renal
function were to suddenly decline to 80% of normal,
the plasma concentration of creatinine would
increase to its new steady state value over 20-25 h
(4-5 times 5 h). Notice that the time to achieve the
steady state depends not upon the normal half-life of
the marker substance but upon the half-life in the
altered physiologic state.
Because of the presence of variability in labora-
tory measurement, the concentration of a marker
Monitoring
5-3
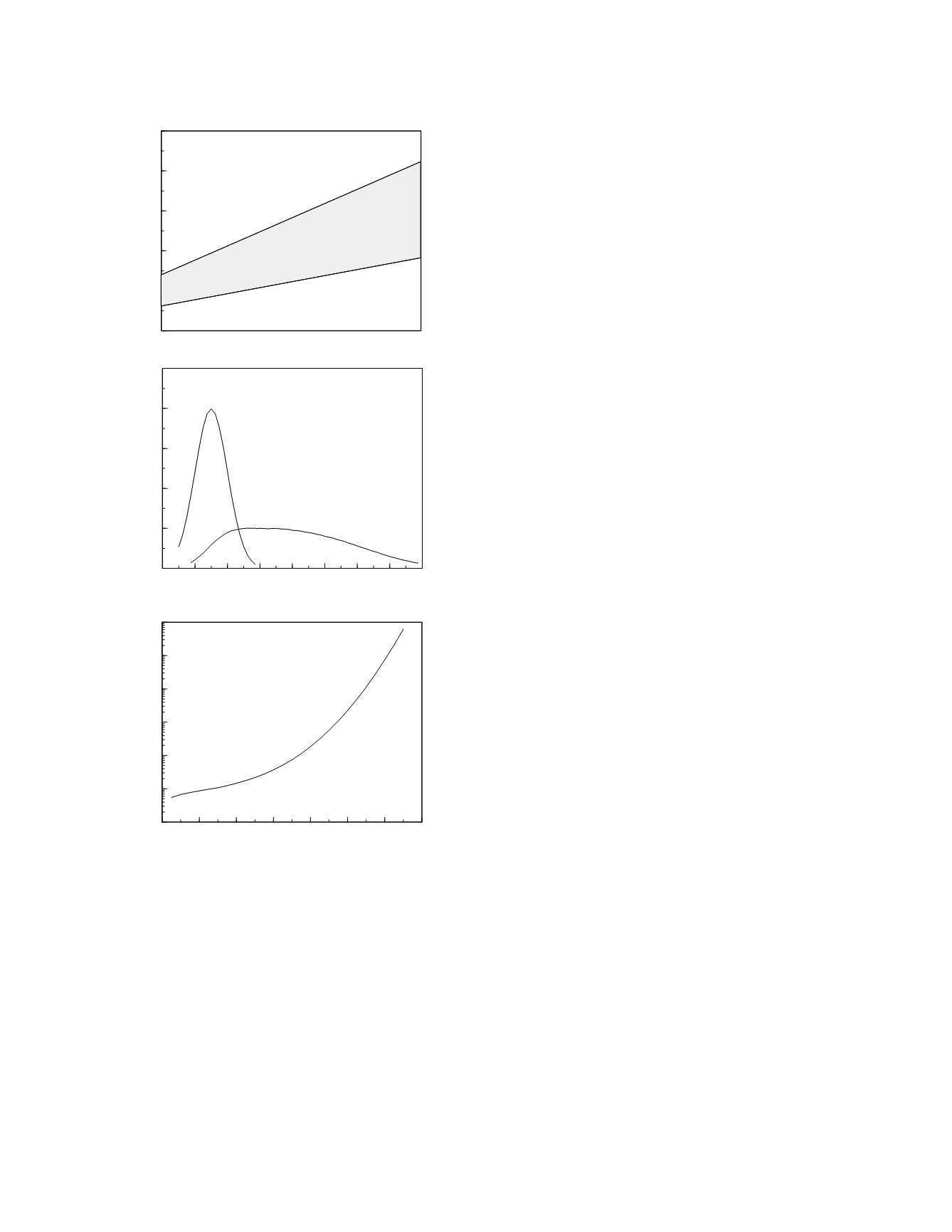
Figure 5.2
The natural history of a diagnostic marker for
the hypothetical disorder (top graph). The classification
characteristics of the marker at year 5 are shown in the
middle and bottom graphs.
Duration of subclinical phase (1 to 5 yr)
0
50
100
150
200
250
Marker concentration
20 40 60 80 100 120 140 160 180
Time (yr)
0
0.01
0.02
0.03
0.04
0.05
Frequency
30 40 50 60 70 80 90 100
Marker concentration
0.01
0.1
1
10
100
1000
10000
Likelihood ratio
subclnical
cases
disease-free
cases
mean + 2 SD
mean - 2 SD


