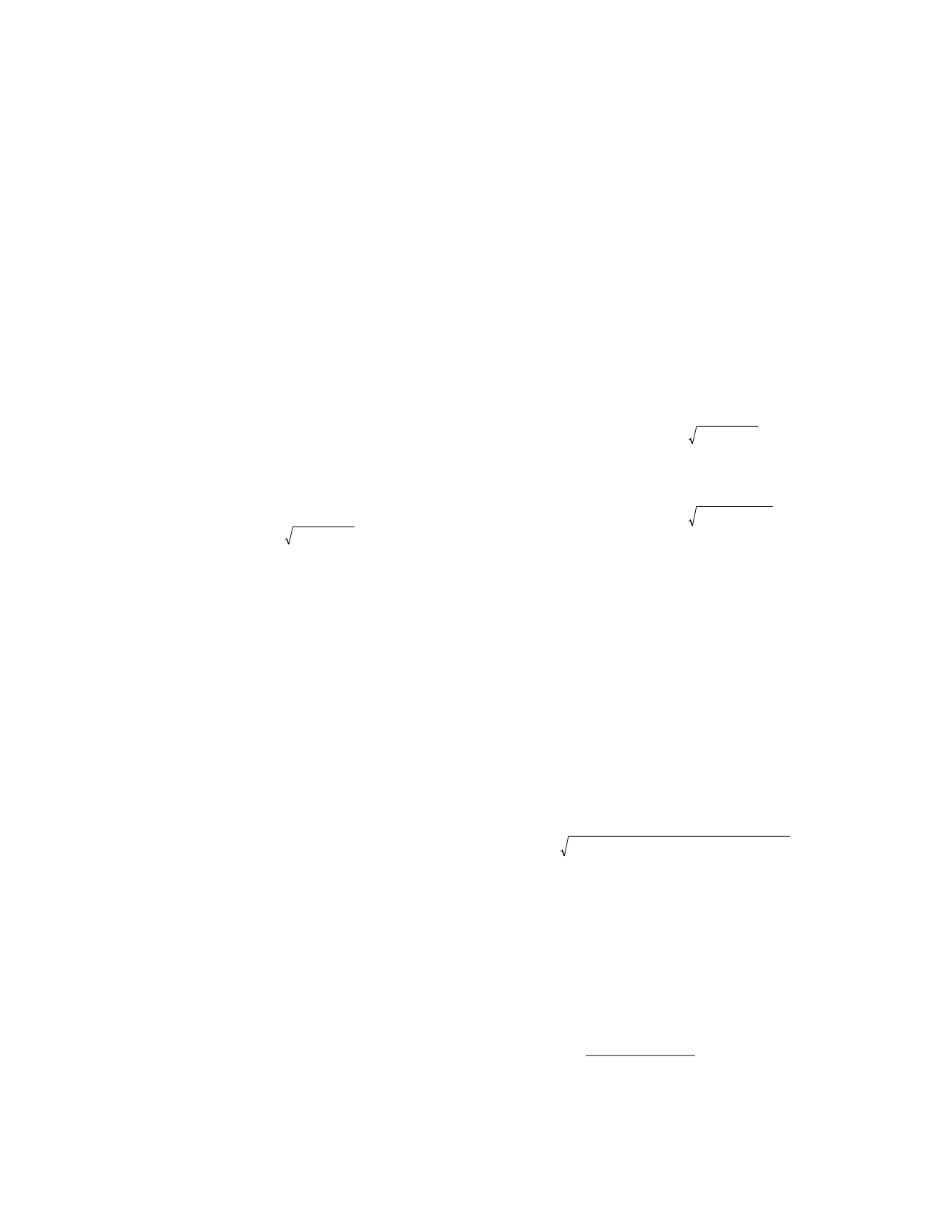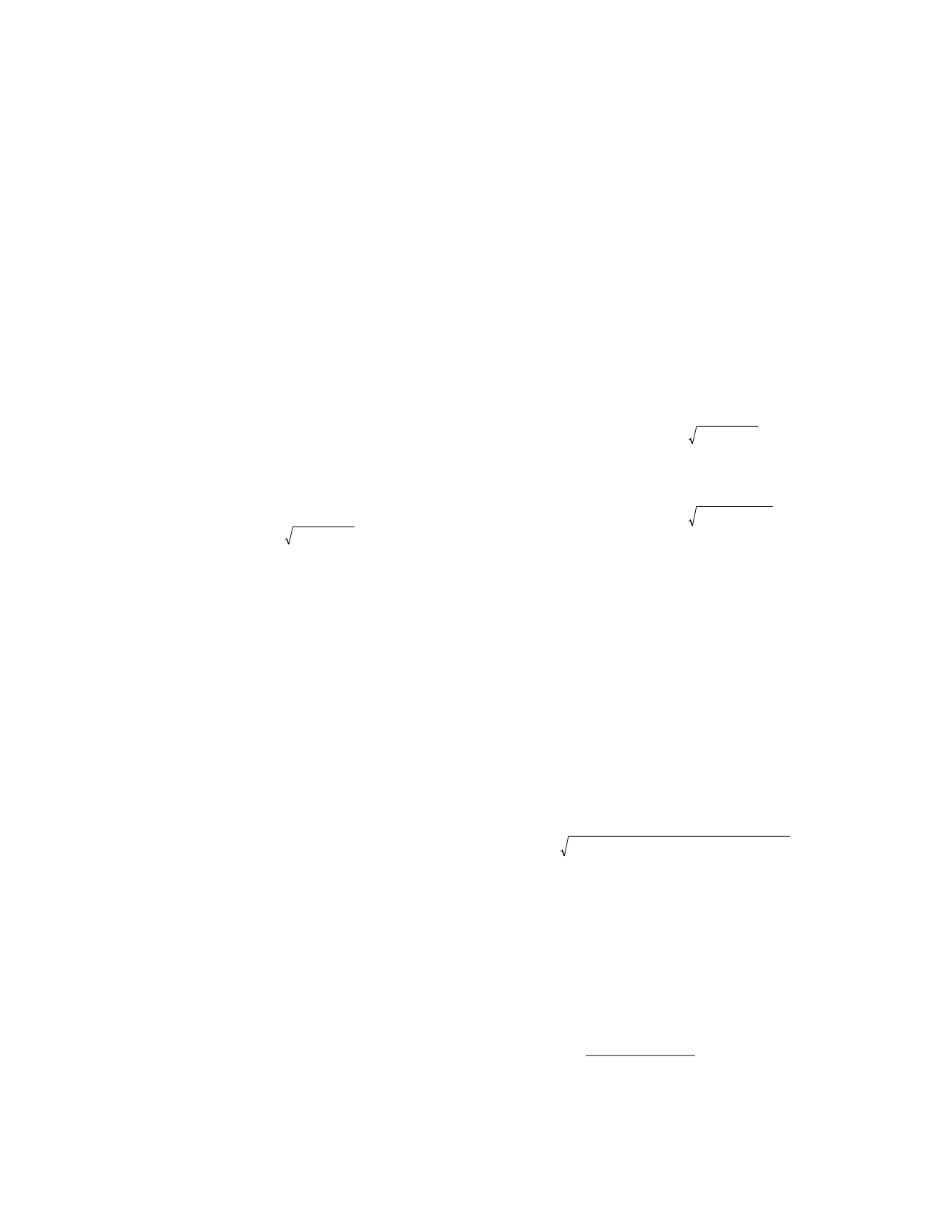
variability, two results will rarely be the same, even
if the patient's physiologic status is unchanged. The
task is to decide if the difference in the results is
more likely due to measurement variability or to a
change in physiologic status.
In the absence of a change in physiologic
function, the study results in an individual are
distributed about some mean value, avg
indiv
, with the
variability characterized by the within-individual
variance, var
indiv
which is the sum of within-
individual biologic variance, var
biologic
, and analytic
variance, var
analytic
. The mean value for the differ-
ence between two measurements is zero and the
variance of the difference is
2
var
indiv
If the specificity for detecting a change in concentra-
tion is set at 0.95, a significantly different value is
one outside the central 95 percent range of the distri-
bution of result differences,
significant difference
m
2 2
var
indiv
Thus, if var
indiv
is 50 µmol
2
/L
2
, for example, an
absolute difference in result values of 20 µmol/L or
more is considered significant, at the stipulated level
of specificity, and implies a change in physiologic
status.
The formula is valid only if the time interval
between measurements is long (Harris and Yasaka
1983) and, for some analytes, only if the interval is
very long (Queraltó
et al.
1993). At shorter inter-
vals the within-individual biologic component of
variability drops out because, for most marker
substances, only small changes in concentration
normally take place over a few hours. Consider, for
example, the blood concentration of neutrophils.
From day to day the concentration can vary as much
as 3x10
9
cells/L around an average value of 3.5x10
9
cells/L. Over a period of 2 to 3 hours, though, the
variability is probably only one-third as great.
Consequently, when measurements are taken at
intervals of less than 3 hours, cell concentration will
show much less variability than when measurements
are made daily. The variability that is present will
be largely analytic.
The degree to which consecutive measurements
are similar due to the sluggishness of biologic
change is embodied in the statistical index, serial
correlation. A serial correlation of one denotes
absolute immobility of the measurement such that
each measurement is identical to its predecessor. A
value of zero indicates that the biologic change is
rapid enough that, at the sampling interval specified,
each measurement appears unrelated to those preced-
ing it. Incorporating the idea of serial correlation,
the variance of the difference between two measure-
ments is,
2
(
1
−
!
(
$
) )
var
biologic
+
2
var
analytic
where
ρ
(
τ
) is the serial correlation for the time inter-
val
τ
.
For most purposes only the two extreme values
for the serial correlation need to be considered.
Either the sampling interval is long relative to the
time needed for a biologic change and
ρ
(
τ
) is equal
to zero, so that,
significant difference
m
2 2
var
indiv
or the interval is short with
ρ
(
τ
) equal to one, in
which case,
significant difference
m
2 2
var
analytic
To use these formulas, estimates of var
indiv
or
var
analytic
are needed. Ideally, these estimates should
be specific for the patient being studied and for the
laboratory in which the analyte is measured. When
there is no antecedent history of study results for the
patient on which to base an estimate of var
indiv
, the
typical value of var
indiv
as found in the medical litera-
ture can be used in its stead. Laboratory staff should
be able to provide values for var
analytic
for the analytes
measured in their laboratory.
For sampling intervals of intermediate length,
serial correlation should be included in the calcula-
tion of the value of a significant difference,
significant difference
m
2 2
(
1
−
!
(
$
))
var
biologic
+
2
var
analytic
remembering that
ρ
(
τ
) refers to the serial correlation
of the biologic component of the measurement
variance. Almost always, the form of serial correla-
tion for which a value is readily available is the total
serial correlation of repeated measurements, r(
τ
).
This statistical parameter depends upon both the
biologic and analytic variability according to the
formula (Harris 1983),
r
(
$
) =
!
(
$
)
var
indiv
−
var
indiv
var
indiv
Substitution of this expression into the preceding
formula and rearrangement shows that when using
total serial correlation,
Monitoring
5-5